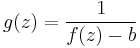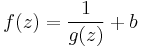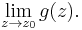Casorati–Weierstrass theorem
In complex analysis, a branch of mathematics, the Casorati–Weierstrass theorem describes the behaviour of meromorphic functions near essential singularities. It is named for Karl Theodor Wilhelm Weierstrass and Felice Casorati.
Contents |
Formal statement of the theorem
Start with some open subset U in the complex plane containing the number z0, and a function f that is holomorphic on U \ {z0}, but has an essential singularity at z0 . The Casorati–Weierstrass theorem then states that
- if V is any neighbourhood of z0 contained in U, then f(V \ {z0}) is dense in C.
This can also be stated as follows:
- for any ε > 0, δ >0, and complex number w, there exists a complex number z in U with |z − z0| < δ and |f(z) − w| < ε .
Or in still more descriptive terms:
- f comes arbitrarily close to any complex value in every neighbourhood of z0.
This form of the theorem also applies if f is only meromorphic.
The theorem is considerably strengthened by Picard's great theorem, which states, in the notation above, that f assumes every complex value, with one possible exception, infinitely often on V.
Examples
The function f(z) = exp(1/z) has an essential singularity at 0, but the function g(z) = 1/z3 does not (it has a pole at 0).
Consider the function
This function has the following Laurent series about the essential singular point at 0:
Because 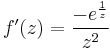 exists for all points z ≠ 0 we know that ƒ(z) is analytic in the punctured neighborhood of z = 0. Hence it is an isolated singularity, as well as being an essential singularity.
exists for all points z ≠ 0 we know that ƒ(z) is analytic in the punctured neighborhood of z = 0. Hence it is an isolated singularity, as well as being an essential singularity.
Using a change of variable to polar coordinates 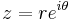 our function, ƒ(z) = e1/z becomes:
our function, ƒ(z) = e1/z becomes:
Taking the absolute value of both sides:
Thus, for values of θ such that cos θ > 0, we have 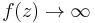 as
as 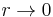 , and for
, and for 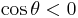 ,
, 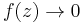 as
as 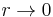 .
.
Consider what happens, for example when z takes values on a circle of diameter 1/R tangent to the imaginary axis. This circle is given by r = (1/R) cos θ. Then,
and
Thus,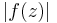 may take any positive value other than zero by the appropriate choice of R. As
may take any positive value other than zero by the appropriate choice of R. As 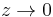 on the circle,
on the circle, 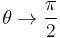 with R fixed. So this part of the equation:
with R fixed. So this part of the equation:
takes on all values on the unit circle infinitely often. Hence f(z) takes on the value of every number in the complex plane except for zero infinitely often.
Proof of the theorem
A short proof of the theorem is as follows:
Take as given that function f is meromorphic on some punctured neighborhood V \ {z0}, and that z0 is an essential singularity. Assume by way of contradiction that some value b exists that the function can never get close to; that is: assume that there is some complex value b and some ε > 0 such that |f(z) − b| ≥ ε for all z in V at which f is defined.
Then the new function:
must be holomorphic on V \ {z0}, with zeroes at the poles of f, and bounded by 1/ε. It can therefore be analytically continued (or continuously extended, or holomorphically extended) to all of V by Riemann's analytic continuation theorem. So the original function can be expressed in terms of g:
for all arguments z in V \ {z0}. Consider the two possible cases for
If the limit is 0, then f has a pole at z0 . If the limit is not 0, then z0 is a removable singularity of f . Both possibilities contradict the assumption that the point z0 is an essential singularity of the function f . Hence the assumption is false and the theorem holds.
References
- Section 31, Theorem 2 (pp. 124–125) of Knopp, Konrad (1996), Theory of Functions, Dover Publications, ISBN 978-0-486-69219-7
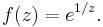
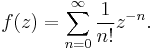
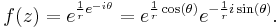
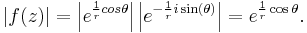
![f(z) = e^{R} \left[ \cos \left( R\tan \theta \right) - i \sin \left( R\tan \theta \right) \right]](/2012-wikipedia_en_all_nopic_01_2012/I/4a07fe0e0d926190b5713a74c1e61ee0.png)
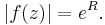
![\left[ \cos \left( R \tan \theta \right) - i \sin \left( R \tan \theta \right) \right] \,](/2012-wikipedia_en_all_nopic_01_2012/I/46981323d8a2b199cd751cb0cb78c137.png)